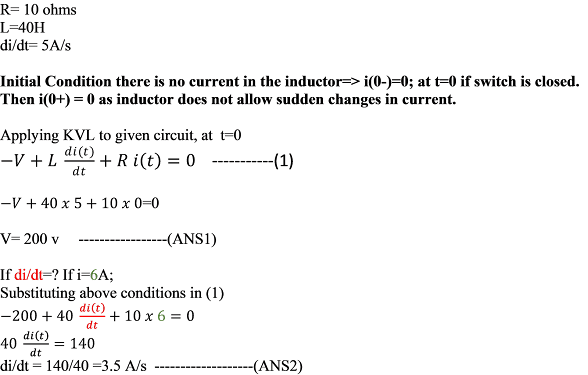NA

R23 Sem Exam Model Paper -PDF LINK

Previous Papers - R20 QP and Key - Link

R23 Syllabus for Network Analysis

Unit-1:
1.1 Types of circuit components
1.2 Types of Sources and Source Transformations
1.3 Mesh analysis and Nodal analysis
1.4 Principle of Duality
1.5 Impedance concept, phase angle, series R-L, R-C, R-L- C circuits, Complex impedance and phasor notation for R-L, R-C, R-L-C
1.6 problem solving using mesh and nodal analysis
1.7 Star-Delta conversion

Unit-2:
2.1 Network Theorems: Thevenin's Theorem
2.2 Norton's Theorem
2.3 Reciprocity Theorem
2.4 Compensation, Substitution Theorems
2.5 Superposition Theorem
2.6 Max Power Transfer Theorem
2.7 Laplace transform: introduction, Laplace transformation, basic theorems

Unit-3(1):
3.1 Transients: First order differential equations, Definition of time constants, R-L circuit
3.2 R-C circuit with DC excitation, evaluating initial conditions procedure
3.3 problem solving
3.4 second order differential equations, homogeneous, non-homogenous, problem-solving using R-L-C elements with DC excitation and AC excitation,
3.5 Response as related to s-plane rotation of roots.

Unit-4:
4.1 Resonance: Introduction, Definition of Q, Series resonance,
4.2 Bandwidth of series resonance
4.3 Parallel resonance and general case-resistance present in both branches, anti-resonance at all frequencies.
4.4 problem solving
4.5 Coupled Circuits: Self-inductance, Mutual inductance, Coefficient of coupling
4.6 analysis of coupled circuits, Natural current, Dot rule of coupled circuits, conductively coupled equivalent circuits

Unit-5: Assignment Key
5.1 Two-port: Relationship of two port networks, Z-parameters
5.2 Y-parameters
5.3 ABCD- parameters
5.4 hybrid parameters
5.4 h- parameters
5.5 Relationships Between parameter Sets
5.6 Parallel, series, cascading of two port networks
5.7 problem solving
5.8 Image and iterative impedances (Qualitative treatment only)

Text Books/ Web References

1. Network Analysis - ME Van Valkenburg, Prentice Hall of India, revised 3rd Edition, 2019.
2. Engineering Circuit Analysis -WilliamH. Hayt, Jack Kemmerly, Jamie Phillips, Steven M. Durbin, 9E

PDF Text Books
1. Engineering Circuit Analysis by Hayt PDF LINK
2. Network Analysis by Sudhakar and Shyammohan PDF LINK

Web References:
NPTEL Course Link

NA Model Problems

KVL model1
KVL model2
KVL model3
KCL model1
KCL Model2
KCL model3
Mesh model1
Mesh model2
Mesh model3
Mesh model4 (Super Mesh)
Mesh model5 (Super Mesh)
Mesh model6 (Super Mesh)
Nodal model1
Nodal model2
Nodal model3
Nodal model4 (Super Node)
Nodal model5 (Super Node)
Duality model1
Duality Model2
Source Transformation model1
Source Transformation model2

Standard AC Signal Waveforms (useful for unit-3)

Material Unit-1: R, L, C- Series and Parallel; KVL and Mesh, KCL and Nodal; Steady State;

-----------------------------------

Basic things when to apply KVL/KCL/Mesh/Nodal:

single loop ----> then use KVL
single node (two ore more loops) ----> then use KCL
two or more loops -----> then use Mesh Analysis
two or more nodes  -----> then use Nodal Analysis

------------------------------------

Cramer's Rule 

KVL

Algebraic sum of voltages in a loop is zero.

-Vs + VR1 + VR2 + VR3 =0

i.e.,

-Vs + I x R1 + I x R2 + I x R3 =0

KCL :  uses I= V/R  or direct value of current source I

Note: if a current source is having a resistor blocking, the R value is neglected.

Algebraic sum of currents at a node is zero.

Here R2 is neglected as it is blocking a current source.

Applying KCL:

(Va -Vs)/R1   +  Va /R4   - I =0

-->

Va [ (1/R1) + (1/R4)] = Vs/R1 + I

-->

Va = {  Vs/R1 + I } / [ (1/R1) + (1/R4)]

Mesh Analysis:
Use of Mesh equations for each loop. If there are 4 loops from left to right.
Then Apply Mesh Analysis (similar to KVL) for the loops as follows: 
Mesh for loop1
Mesh for loop2
Mesh for loop3
Mesh for loop4

Ex:

Mesh  for Loop1:

-Vs + I1 (R1) + (I1 -I2) R3 =0 

-->

 I1 (R1+R3) -I2 (R3) =Vs    ---(eq1)

Mesh for loop2:

(I2- I1) R3 + I2 (R2) + I2 (R4) =0

-->

-I1( R3) + I2 (R2+R3+R4) =0  ---(eq2)

solve eq1 and eq2 using Cramer's Rule to determine I1 and I2.

Nodal Analysis:

Use of Nodal Analysis at each node. If there are three nodes from left to right.

Then Apply Nodal Analysis (similar to KCL) for nodes as follows: 
Nodal Equation for node1
Nodal Equation for node2

Nodal Equation for node3

Nodal Equation for node4

Ex:

Nodal Equation at Va:

(Va- 15)/4700  + Va/ 2200 +  (Va - Vb)/470  =0 

-->

 Va [ (1/4700) + (1/2200)+ (1/470)]  + Vb (-1/470) = (15/4700)      ----(eq1)

Nodal Equation at Vb:

 (Vb - Va)/470  + Vb/ 50  - 0.01  + Vb /(100+500)  =0 

-->

  Va(-1/470)  + Vb [(1/470) + (1/50)+ (600)] = 0.01      ----(eq2)

solve eq1 and eq2 using Cramer's Rule to determine Va and Vb.

Duality:

The dual elements for each element are as follows:

R <---> G

L<-----> C

V <-----> I

Shortcuts only(for quick work)

• Series elements become parallel elements between nodes and vice-versa
• horizontal elements become vertical elements between nodes and vice-versa

Source Transformation:

if there is a current source, then to transform it to voltage source use V= IR 

OR

if there is a voltage source, then to transform it to current source use I= V/R

Star Delta:

let delta elements be Ra, Rb, Rc

let Star elements be R1, R2, R3

then if we know Delta values, then it needs to be transformed to Star

Delta to Star

R1 = Ra Rb/ (Ra +Rb+ Rc)

OR

then if we know Star values, then it needs to be transformed to Delta

Star to Delta

Ra= (R1 R2+ R2 R3 + R1 R3)/R2

Steady State and Transient Comparison:

Transient refers to a temporary or short-lived condition. In the context of systems or processes, transient state refers to the period of time during which the system is adjusting to a change or disturbance. It is the time it takes for the system to reach a new equilibrium or steady state after being subjected to a change.

Steady state, on the other hand, refers to a stable and unchanging condition. In the context of systems or processes, steady state refers to a situation where the system's variables do not change over time, or where any changes are balanced by other factors, resulting in an overall equilibrium.

In summary, transient state refers to a temporary or adjusting condition, while steady state refers to a stable and unchanging condition.

Complex Impedance Concept:

---------------------------

Let

Vs = Vm ejωt

Is = Im ejωt

--------------------------

applying KVL

-Vs+ VR + VL + VC =0

=>

Vs =VR+VL+VC

---------------------------

Let

Vs = Im ejωt R + L d/dt(Im ejωt ) +(1/C)∫ Im ejωt dt

taking Im common on LHS

Vs = Im { ejωt R + L d/dt( ejωt ) +(1/C)∫  ejωt dt}

applying differentiation and Integration to respective terms

Vs = Im { ejωt R + jωL  ejωt+ (1/C) ejωt/(jω) }

taking common ejωt 

Vm ejωt = Im  ejωt{  R + jωL  + (1/(jωC) } 

writing as real and imaginary terms

Vm = Im  {  R + jωL  + (1/(jωC) }

Vm = Im { R+j(X_L-X_C)} 

where X_L=ωL   and

X_C=1/(ωC)

X_L and X_C are called Reactance of inductor and capacitor respectively.

i.e., Vm = Im Z where Z= R+j(X_L-X_C)

--------------------------

Phase angle concept:  

Assume a series R-L Circuit.

Let

v(t) = Vm sinωt ; 

i(t) = Im sinωt ;

-------------------------

Voltage across inductor is

 v'(t) = L di(t)/dt

-->   v'(t) = L d(Im sinωt )/dt   

-->    v'(t) =Im L d( sinωt )/dt

-->  v'(t) =Im L ω cosωt

--> v'(t) =Im L ω cosωt

--> v'(t)= Im X_L  sin(90+ωt)

where X_L = ω L

So if current is sinωt then voltage leads current by 90

-----------------------------

V leads I by 90º

means inductor does not allow sudden changes in current;

so I lags

both phase diagrams are correct.

if V on Y axis, then current must lag by 90

similarly if V on X-axis, I must lag by 90

i.e., V always leads I by 90

----------------------------

similarly for a resistive network, V and I are in phase always.

similarly you can prove, for a series R-C circuit: V lags I (OR) I leads V

similarly for a series R-L-C circuit: V & I phase relation depends on X_L and X_C Values.

Quiz Unit-1

1. Resistance has unit of  ______

2. Capacitance has unit of  _____

3. Inductance has unit of _____

4. Resistors R1, R2 and R3 are connected in series ;  the equivalent value is _____

5.  Resistors R1, R2 and R3 are connected in parallel;  the equivalent value is _____

6. Inductors L1, L2 and L3 are connected in series ;  the equivalent value is _____

7.  Inductors L1, L2 and L3 are connected in parallel;  the equivalent value is _____

8. Capacitors C1, C2 and C3 are connected in series ;  the equivalent value is _____

9.  Resistors R1, R2 and R3 are connected in parallel;  the equivalent value is _____

10.  for below network, RAB  = _______ ohms

11. f=10kHZ, L= 0.1mH ; Reactance of inductor =  ______ Ω

12. f=10kHZ, C= 10µH ; Reactance of inductor =  ______ Ω

13. R=100Ω, L= 0.08mH, C=9nF; frequency =1MHz;

R, L, C are connected in series; then the impedance is  _____

14. In inductor V   _____  I

15. In capacitor V ______ I

16. If two current sources are connected in parallel (both current directions pointing upwards), then the equivalent current value is ______

17. If two current sources are connected in parallel (one current direction pointing upwards, another pointing downwards), then the equivalent current value is ______

18. 1+j = ___________in the form of r∠θ

19. 5+3j =  _________   in the form of r∠θ

20. 5∠90 = ________ in a+jb form

21.  7∠45 = _______ in a+jb form

Key for Model Quiz-1:

1. Ohm

2. Farad

3. Henry

4. R1+R2+R3

5. (1/Req) = (1/R1)+(1/R2)+(1/R3) 

or

Req = [ (1/R1)+(1/R2)+(1/R3) ]-1

6. L1+L2+L3

7. (1/Leq) = (1/L1)+(1/L2)+(1/L3) 

or

Leq = [ (1/L1)+(1/L2)+(1/L3) ]-1

8. (1/Ceq) = (1/C1)+(1/C2)+(1/C3) 

or

Ceq = [ (1/C1)+(1/C2)+(1/C3)  ]-1

9. Ceq= C1+C2+C3

10. 1.5 

11.  j6.283

12.  -j1.591

13. 100 + j502.654   - j17.683 = 100+j484.971

14.  Leads

15.  lags

16. sum of both the currents

17. difference of the currents

18. 1.414∠45

19. 5.83∠30.96

20. 5j

21. 4.949+4.949j

Assignment Questions Unit-1

1. Explain about the classification of sources.

2. Determine the voltage across 4.7kΩ. Use network in figure-1.1

3. Simplify the given network (figure-1.2) to single current source and a resistor using Source transformation technique.

4. Use figure-1.3; Determine the current in 1kΩ resistor using Mesh Analysis/Nodal.

5. (a) Determine the complex impedance of a series R-L-C circuit.

    (b)Draw the phasors for V vs I, in case of a series R-L-C circuit.

6. Determine the duality of the network given in figure-1.4.

7. Determine the current in 800Ω of network given in figure-1.5, using Mesh/Nodal Analysis.

8. Write the Mesh/Nodal equations for the network shown in figure-1.6.

9. Use star-delta/vice-versa transformation to obtain the equivalent resistance between A and B for the network shown in figure-1.7

Assignment Key Unit-1

2.

Assume clockwise current I.
Apply KVL:
-13+200I+4700 I+ 3+470 I+330 I+ 10000 I=0
15700 I = 10
I= 0.000636942 A = 636.942µA

3.

Current source from voltage source --> 120/20 = 6A Current source from voltage source-->60/5 = 12A 1.6 in series with 8-->9.6Ω

Overall current = 6-12+36 = 30A

4.

Mesh Analysis Technique:

from the figure, I₃ =5A    ---(1)

Applying Mesh for loop1: -10+1000 I₁ + 4700(I₁-I₂)-8 =0          ---(2)

Applying Mesh for loop-2: 8+ 4700(I₂-I₁) +100 I₂+10+5(I₂+I₃) =0         ---(3)

solving (2), (3) equations using Cramer’s Rule:

I₁= -21.819mA, I₂= -30.291mA

Current in 1kΩ resistor is I₁ i.e.,  -21.819mA

Nodal Analysis Technique:

applying Nodal analysis to nodes Vx and Vy:

5. 

step-1: place nodes inside each loop and a reference node at the ground (outside the loops)

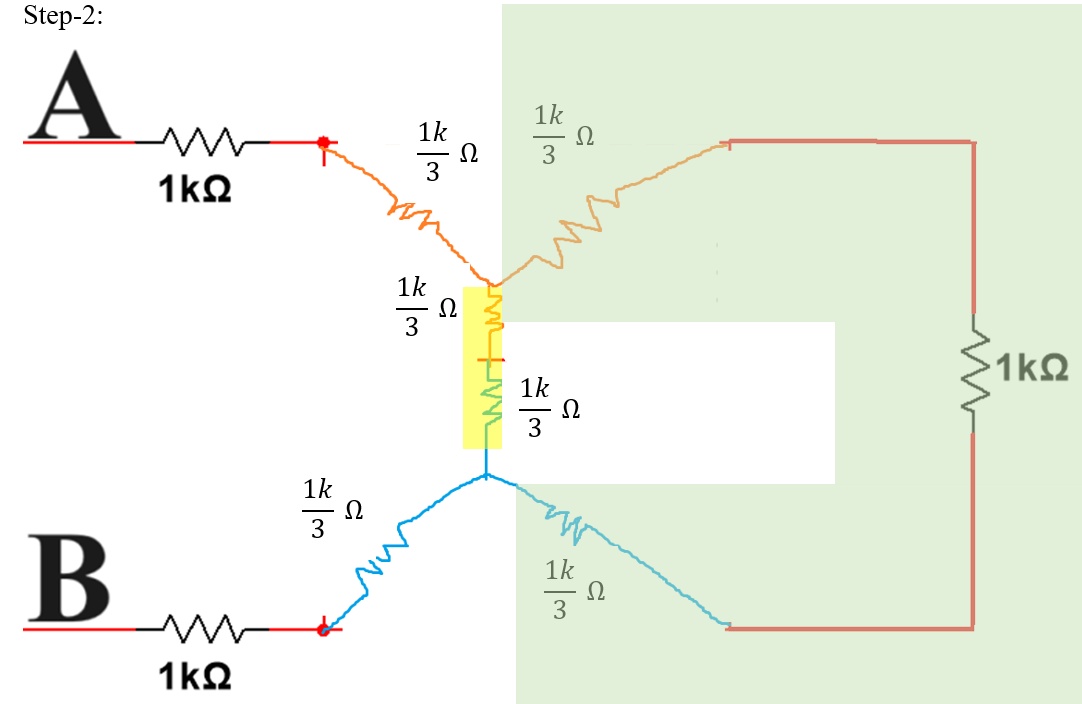
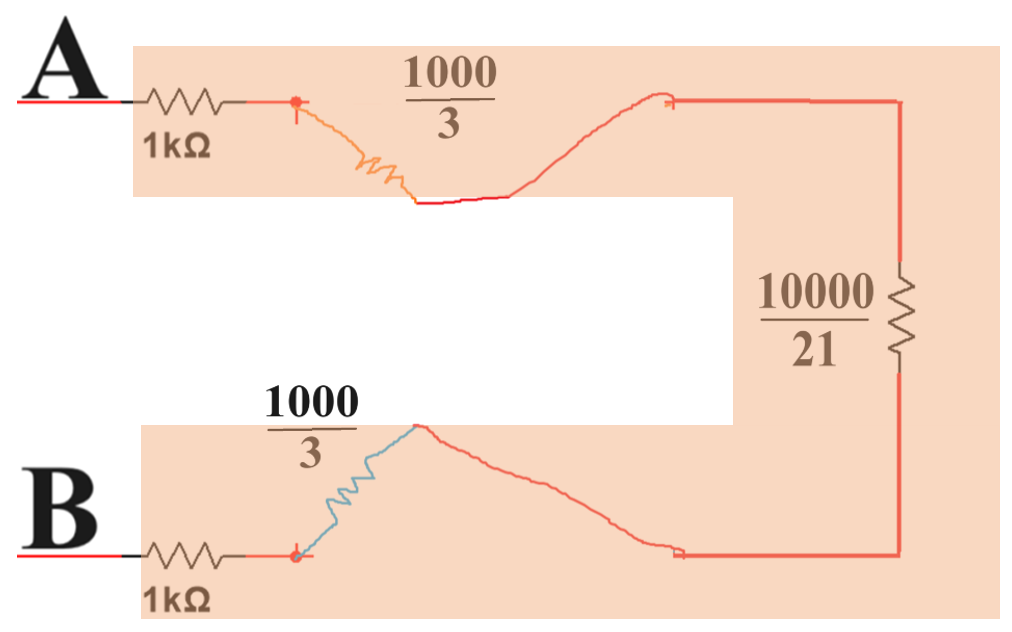
step-2: connect each node inside loop and ref_node via elements in that loop only. replace the elements with their dual element.

step-3: continue the step2 for nodes inside remaining loops also.

Step-4: draw the final dual figure

6. 

Mesh analysis:

Mesh at loop1:

-8+I1(j3) – j2(I1-I2) =0     ---(1)

Super Mesh at loop2, loop3:

-j2(I2-I1)+ 7 I2 + 800 I3 = 0    ----(2)

at current source:

I3-I2= 1A  ----(3)

Solving equations (1), (2) and (3) using Cramer’s Rule:

I₁= 2.022-7.984j = 8.236 ∠ -75.788 A

I₂= -1.011-0.007517j = 1.011∠ -179.57 A

I₃= -0.011096-0.007517j =0.0134∠ -145.884 A

Current in 800Ω is I3 i.e., 0.0134∠ -145.884 A

Nodal Analysis Technique:

Solving (1) and (2) equations using Cramer’s Rule

Vx = 15.954-6.0666j 

Vy = -8.877-6.0139j V

Current in 800Ω is Vy/800 = 0.013∠ -145.884 A

7. 

before solving mesh/nodal here all the inductors/capacitors must be replaced with their reactance values respectively.

f=1000 Hz

ω= 2πf = 6283.1853 rad/s

20mH-->jωL = j125.663 Ω 

1µF--> -j/(ωC)= -j159.154 Ω

Mesh Equations:s:

Mesh at loop1:

-12+ I1(j125.663 ) - j159.154 (I1-I2)=0   ---(1)

Super Mesh at loop2, loop3:

-j159.154  (I2-I1) + 47 I2 +470 I3 =0  ---(2)

 Evaluating Current source:

I3-I2= 0.7 ---(3)

Nodal Equations:

8. 

STEP-1:

convert respective delta to star:

STEP-2:

STEP-3:

STEP-4:

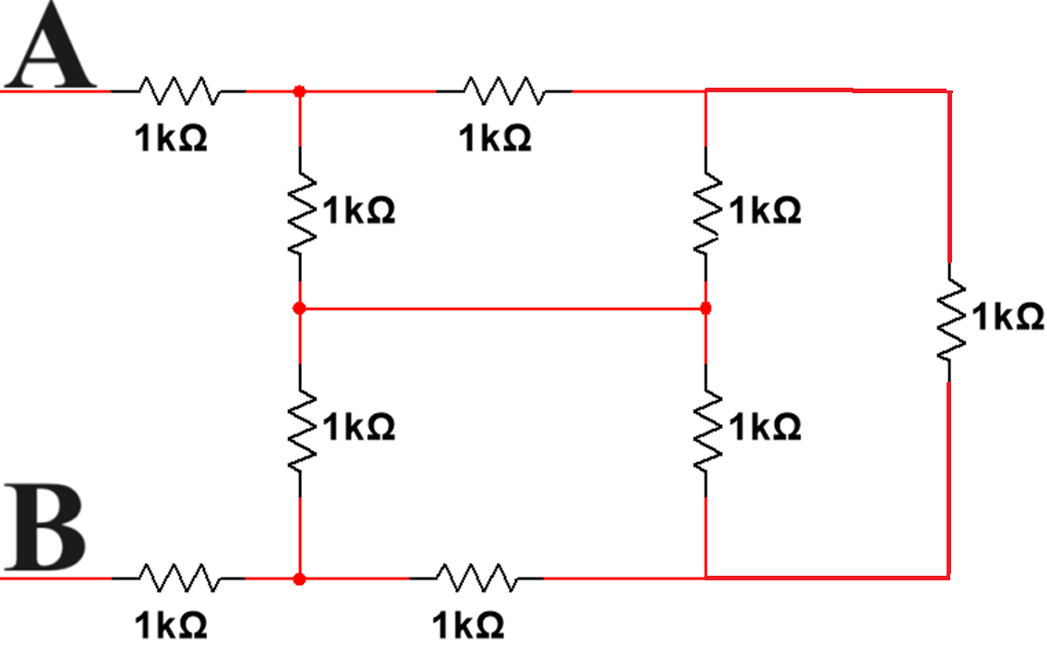
ANS:  22000/7 = 3142.857Ω = 3.143kΩ

Material Unit-2: Network Theorems, L.T, I.L.T and Partial Fractions

Thevenin's Theorem

It is possible to simplify any linear circuit, irrespective of how complex it is, to an equivalent circuit with a single voltage source and a series resistance. V_Th and R_Th  are in series to the load R_L.

Norton's Theorem

Any complex linear circuit can be simplified to an equivalent simple circuit with a single current source in parallel with a single resistor connected to a load.  I_N and R_Th  are in parallel to the load R_L.

Reciprocity Theorem

Reciprocity in electrical networks is a property of a circuit that relates voltages and currents at two points. The reciprocity theorem states that the current at one point in a circuit due to a voltage at a second point is the same as the current at the second point due to the same voltage at the first.

Substitution Theorem

Substitution Theorem states that any branch of a DC bilateral circuit can be substituted by a combination of various circuit elements, provided the current & voltage across the branch remains unchanged.

Maximum Power Transfer Theorem:

case (i): if its purely resistive network

===>     then Z_s= R_s = R_Th and Z_L=R_L

i.e., R_Th = R_L

case (ii): if its complex impedance network

if Zs= R+jX then Z_L =?

dP_L/dX_L) = 0 is part1 of solution

dP_L/dR_L) = 0 is part2 of solution

Compensation Theorem:

The compensation theorem tells that with the change of branch resistance, branch currents changes and the change is equivalent to an ideal compensating voltage source in series with the branch opposing the original current, all other sources in the network being replaced by their internal resistance

Superposition Theorem:

Superposition theorem states that in any linear, bilateral network where more than one source is present, the response across any element in the circuit is the sum of the responses obtained from each source considered separately. In contrast, all other sources are replaced by their internal resistance if given.

Laplace Transform (LT)and Inverse Laplace Transform (ILT) Properties

Laplace Transform of f(t)==> L.T{f(t)}

₀∫∞ f(t) e–st  dt = F(s) is a Unilateral integral (mostly used)

-∞∫∞ f(t) e–st  dt = F(s) is a Bilateral integral

-------------------------------

Laplace transform of f(t) i.e.,   f(t)  ----LT ---> F(s)

 Inverse Laplace Transform of F(s) i.e.,  f(t)  <---ILT-----F(s)

time  <----> s domain

f(t)    <----> F(s)

--------------------------------

1   --> 1/s

10 --> 10/s

a  ---> 1/s   where a is constant

δ(t)  --> 1

---------------------------------

e–at  ---->1/(s+a)

eat  ---->1/(s–a)

--------------------------------

sin(bt)  -----> b/(s2+b2)    where b is constant

cos(bt)  -----> s/(s2+b2)    where b is constant

sinh(bt)  -----> b/(s2– b2)    where b is constant

cosh(bt)  -----> s/(s2–b2)    where b is constant

--------------------------------

if f(t) <----->F(s)

then

e–at   f(t) ----->F(s+a)

OR

eat   f(t) ----->F(s–a)

--------------------------------

Applying above theorem 

Ex:

e–at   f(t) ----->F(s+a)

e–at   sin(bt) ----->F(s+a) ---> b/((s+a)2+b2) )

eat   cos(bt) ----->F(s–a) ---> (s–a)/((s-a)2+b2) )

-------------------------------

L.T {∫ f(t) dt } -----> F(s)/s

L.T {f '(t)} -----> sF(s) – f(0+)

L.T{f "(t)} ------> s2 F(s) – s f(0)  –f '(0+)

---------------------------------

Quiz Unit-2

1. V_Th  and R_Th  in Thevenin's equivalent are in _______ (series/parallel).

2. I_N  and R_Th  in Norton's equivalent are in _______ (series/parallel).

3. Reciprocity Theorem must contain maximum of  _______ sources.

4. Superposition Theorem must contain minimum  of _______ sources.

5. __________theorem uses simple formula to replace an element as either voltage source or current source.

6. In Thevenin's Theorem, to calculate V_Th, the load across A and B terminals is  _____ (O.C/ S.C)

7. In Norton's Theorem, to calculate I_N, the load across A and B terminals is  _____ (O.C/ S.C)

L.T = Laplace Transform = L { }

I.L.T = Inverse Laplace Transform =   L^-1{  }

8. L^-1{ 1/(s+4)  } = ______

9.   L^-1{ 1 } = ______

10. L { 1 }= ______

11.   L^-1{ 1/9 } = ______

12.   L^-1{ s/(s+1) } = _______

13.   L^-1{ s²/(s²+4) } = _______

Key for Model Quiz-2:

1. series

2. parallel

3. single  or  one

4. two

5. Substitution 

6. O.C

7. S.C

Note: O.C = Open Circuited , S.C = Short Circuited

8.  e^-4t

9. δ(t)

10. 1/s

11. (1/9) δ(t) 

12.  =   L^-1{  1 - [1/(s+1)] } = δ(t) - e^-t

13. =   L^-1{  1 - [4/(s²+4)] } = δ(t) - 2 sin2t

Assignment Questions Unit-2

Figure2.1  for Questions 2 to5

Figure2.2  for Questions 6,7

1. Determine the condition such that maximum power is delivered to the load with a neat sketch.

2. Determine the Thevenin’s equivalent across RL, for network in figure-2.1

3. Determine the current in 470Ω of figure-2.1 using Norton’s Theorem if RL =10kΩ.

4. For figure-2.1, Determine the RL such that maximum power is delivered to it.

5. For figure-2.1, determine the current in 2.2kΩ resistor using Superposition Theorem. Assume RL =10kΩ. 

6. if RL=1.5kΩ in figure-2.2, then prove reciprocity theorem in case of 1kΩ resistor.

7. Use figure-2.2, State and prove substitution theorem, at RL. Assume RL=50 Ohms.

8. Determine the function f(t), if 

9. Determine the function x(t), if 

Assignment Key Unit-2

I= Vy/ 1000= 1.139mA

Step 2: 

Now interchange source and response positions

Applying Nodal analysis

Va/4700 + Va/2200 + (Va-Vb)/470 =0

(Vb-Va)/470+ (Vb-15)/1000 + Vb/1600=0

Va= 5.353375V

New response

I' = Va/4700= 1.139mA

Q7.

 

                     

Material Unit-3: Transients

A loop if contains only L or only C is first order circuit; if a loop contains both L and C = second order circuits.
Example: RC circuit is 1st order; RL circuit is 1st order circuit; RLC is a 2nd order circuit;

Topics:
1. Initial Conditions
2. Revise topics L.T, I.L.T, Partial Fractions in Unit-2 Part-2
3. DC (step) excited circuits - RC, RL, RLC : here to calculate time constant(𝜏) i(t), v(t), etc.,
4. AC (Impulse, Ramp, Sine, Cosine) excited circuits - RC, RL, RLC : here to calculate i(t), v(t), etc.,
5. di/dt , d^2i/dt^2 problem solving

Evaluating Initial Conditions:

element	t=0+	t=∞
R- Resistor	R	R
L- Inductor	open circuit	short circuit
C- Capacitor	short circuit	open circuit

 

I order circuits (Ex1: Series RC, Ex2: Series RL, ...)

1(a) Series RC with DC Excitation- Differential Equation Method:

Assume there is no initial voltage in capacitor.

1(b) Series RC with DC Excitation- Laplace Transform Method:

Figure showing the current i(t) for series RC.

Now to calculate voltage across capacitor:

2(a) Series RL circuit with DC Excitation:

II order Circuit:

Problems and Solutions:

#1 

A capacitor of 12 pF is to be charged and is designed such that the time taken by the capacitor voltage to reach 90% of its final value should not exceed 3 ns. Find the maximum value of resistance that may be used. 

Solution:

#2 

The values of R and L in a series R–L circuit are 10 ohms¬ and 40 H, respectively. At the instant of closing the switch, the current rises at the rate of 5 A/s. Calculate the following:

i. the value of applied voltage

ii. rate of growth of current when 6A flows in the circuit

Solution:

#3: 

A circuit has resistance of 1000 ohms and a series capacitance of 0.1μF. At t = 0, it is connected to a 12 V battery. Determine the following:

i. The current at t = 0

ii. Rate of change of current at t = 0

iii. Rate of change of capacitor voltage at t = 0

iv. Current at t = 0.1 ms

v. Voltage across capacitor at 0.1 ms

Solution:

#4

A DC voltage of 20 V is applied in an R–L circuit where R = 5 ohms and L = 10 H. Calculate 

i. the current i

ii. voltage across resistor and voltage across the inductor

iii. the time constant and 

Solution:

 

Quiz Unit-3

1. For the given circuit, the switch is closed at t=0; Assuming zero initial conditions, current through inductor at i(0+) = ______ amperes

2. Assume zero initial conditions. Vs =10 V, R =50 ohms, C =100uF. The current through the network elements i(t)= ______________ Amperes

3. For the given I(s), i(t) = _______ A

4. Laplace transform of  Inductor of 2mH is _____

 

5. Laplace transform of Capacitor of 1uF is _____

6. Laplace transform of source Vs = 20 V is ______

 

7. Laplace transform of source di(t)/dt is ______

 

8. Laplace transform of source ∫i(t) dt is ______

 

Q 9, 10 are linked answer Questions:

9. for the given circuit, KVL is _____________

 

10. for the above KVL , Laplace transform is __________________

 

 

Answers:

1. i(0+) =0 A

2. 0.2 e^-200t A

3. 2 e^-3t  - 4  e^-2t A

4. 2x 10^-3 s

5.  1x 10^-6 / s

6. 20 /s

7. s I(s) - i(0)

8.  I(s) /s

 

9.

 

10. 

Assignment Questions Unit-3

Due date: 13/4/2024

1. Compare Steady state analysis and Transient analysis.

2. Determine the time constant of a series R-C network with DC excitation.

3. Determine the time constant of a series R-L network with DC excitation.

4. use figure-3.1; Determine the inductor voltage for t >0.

 

5. For figure-2, Also the switch is open for a long time and closed at t=0. 

Determine di₁(t)/dt, di₂(t)/dt  at t=0+.

 

6. use figure-3.3; Determine v(t) at t=0 and t=160µs

7. For the below series RLC circuit: Let  V1= 20V, R=100 ohms, C1= 20uF, L1= 50mH; determine loop current i(t)

8. For the below RLC circuit: V1= 10V, C1= 20uF, R1= 10 ohms, R2= 10 ohms, L=1H; Switch is closed at t=0; Determine i1, i2, di1/dt, di2/dt,  d2i1/dt2, d2i2/dt2  at t=0+

9. For the below RLC circuit: Let V2= 200 cos(500t+ 45o ), R2=30 ohms, L2=0.2H, C2=6uF; switch is closed at t=0; determine i(t);  

Assignment Key Unit-3

1. Compare Steady state analysis and Transient analysis.

Circuit Behavior is classified as SteadyState (Forced Response) and Transient State (Natural Response).

In summary, transient state refers to a temporary or adjusting condition, while steady state refers to a stable and unchanging condition.

Example: Voltage changes across a capacitor. It is in transient state during charging state with typical exponential curve, and gets to steady state when it is fully charged

Steady State : The circuit parameters like voltage, current across elements (like R, L, C) do not change with respect to time. Steady state, on the other hand, refers to a stable and unchanging condition. In the context of systems or processes, steady state refers to a situation where the system's variables do not change over time, or where any changes are balanced by other factors, resulting in an overall equilibrium.

Transient State: The circuit parameters like voltage and current across elements (like R, L, C) change with respect to time. This behavior is caused by the already charged / discharging behavior of L and C as  the circuit has been put under test (like Turn ON and OFF switch, etc.,). Also it refers to a temporary or short-lived condition. In the context of systems or processes, transient state refers to the period of time during which the system is adjusting to a change or disturbance. It is the time it takes for the system, to reach a new equilibrium or steady state after being subjected to a change.

2. Determine the time constant of a series R-C network with DC excitation.

Solution:

Step-1: Assume Initial condition of Capacitor: Zero Initial condition i.e., Vc(0)=0V means that, there is no voltage across capacitor initially.

Also the switch is closed at t=0;

Hence Vc(0) = Vc(0+)= 0V;

Step-2: KVL for the circuit:

-Vs + i(t) R + (1/C)∫i(t) dt =0

Apply Laplace Transform

-Vs/ s + I(s) R +(1/C) I(s) / s =0

I(s) =  -Vs/ s / [R+(1/CS)]

3. Determine the time constant of a series R-L network with DC excitation.

use similar approach followed in Q2.

4. use figure-3.1; Determine the inductor voltage for t >0.

 figure-3.1

t<0  --> After a long time with switch at this position, Inductor acts as S.C; 10V appears across 4Ω resistor. So current I_4Ω  = 10/4 =2.5A = i_L

at t=0 switch is moved ---> voltage source disconnected at top terminal; So it experienced O.C. 

As inductor does not allow sudden changes in current, i_L(0+) =2.5A

Applying KVL, 10i_L+v= 0  ---(1); 

Also v=5di_L/dt    ---(2);

substitute (2) in (1) --> 10i_L + 5di_L/dt = 0    ---(3)

applying Laplace Transform for Eq(3):

10 I(s) + 5 [sI(s)-i(0)] =0

10 I(s) + 5[sI(s)-2.5]=0

2 I(s) + [sI(s)-2.5] =0

I(s) [2+s] = 2.5

I(s) = 2.5/ (s+2)

Applying Inverse Laplace Transform to I(s):

L^-1{2.5/(s+2)} ---> 

        i(t) = 2.5 e-2t    ----(4)

substitute (4) in (2) ---->

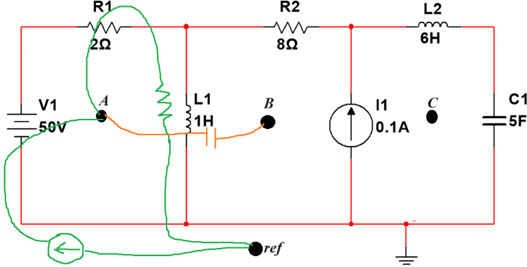
5. For figure-3.2, Also the switch is open for a long time and closed at t=0. Determine di1(t)/dt, di2(t)/dt at t=0+.

 

figure-3.2

until t<0 --->  i_2H(0-) = 0A

i_5H(0-) = 0A because there is no source in the second loop.

as inductor does not allow sudden changes in current, i1(0+)=0A, i2(0+)=0A

6. use figure-3.3; Determine v(t) at t=0 and t=160µs

 

figure-3.3

Before the switch moves (t<0), the 80Ω  resistor is not connected completely (i.e., i=0. Also Assuming that switch position there from long time i.e., capacitor fully charges and there is no path for discharge. 

So, v(0-)= 50 V 

switch position is changed at t=0; As capacitor cannot discharge instantly (capacitor does not allow sudden changes in voltage), v(0+) =50V

now the new circuit is RC network.

time constant is τ=RC = 80 x 2µ = 160µs

voltage across capacitor is, v(t) = v(0) e-t/τ

--->  v(t) = 50 e-t/(160µ) Volts      ----(1)

(a) v(0) --->  t=0 in equation(1) --->  50 e⁰ = 50 volts

(b) v(160µs) = 50 e^{-(160µ)/(160µ)}  = 50 x e^-1  = 18.3939V

7. For the below series RLC circuit: Let  V1= 20V, R=100 ohms, C1= 20uF, L1= 50mH; determine loop current i(t)

Ans: 

Applying KVL

-20 + 100 i(t) + 50m di/dt + (1/20u) integral i dt=0

Applying Laplace transform:

-20/s + 100I(s) + 50m [sI(s) -i(0+)] + (1/20u) I(s)/s =0

Rearranging terms

I(s) = (20/s) / { 50m (s^2+ 2000s + 10^6) }

Applying inverse Laplace transform:

i(t) = 400t e^-1000t Amperes

8. For the below RLC circuit: V1= 10V, C1= 20uF, R1= 10 ohms, R2= 10 ohms, L=1H; Switch is closed at t=0; Determine i1, i2, di1/dt, di2/dt,  d2i1/dt2, d2i2/dt2  at t=0+

Solution:

 i1(0+) =1A

i2(0+)=0A

di₁/dt at t=0+ = -4990 A/s

di₂/dt at t=0+ = 10A/s

d²i₁/dt² at t=0+ =24899900  A/s²

d²i₂/dt²  at t=0+ = -50100  A/s²

9. For the below RLC circuit: Let V2= 200 sin(500t+ 0°), R2=30 ohms, L2=0.2H, C2=0F; switch is closed at t=0; determine i(t);  

Ans:

i(0)=0A ---> i(0+)=0A

Apply KVL for the given network

-200 sin(500t) + 30 i(t) + 0.2 di/dt =0

Apply Laplace Transform 

-200 *500/(s² +500²) + 30 I(s) + 0.2 [ sI(s)-i(0+)]=0

Simplifying

I(s)= 5x10⁵ [ 1/(s² + 500²) x 1/(s+150) ]

Applying partial fractions

I(s)= (As+B)//(s² +500²)  + C/(s+150)= 5x10⁵ [ 1/(s² +500²) x 1/(s+150) ]

If s=-150, C=200/109

Comparing s² coefficients:

A+C=0 ---> A=-C ----> A= -200/109

Comparing s coefficients:

B+150A=0

B=-150A= -30000/109

C= 200/109

A= -200/109

B= -30000/109

Applying inverse Laplace Transform 

i(t)= [-200/109] cos500t - [60/109] sin500t + [200/109]  e^-150t

Note: if source is 200 cos(500t) then 

i(t)= [60/109] cos500t +1.834 sin500t - [60/109] e-150t

Material Unit-4: Resonance and Coupled Circuits

Topics:
1. Resonance:
(a) Series Resonance (ωo, ω2, ω1, BW, Q)
(b) Parallel Resonance (ωo, ω2, ω1, BW, Q)
(c) Parallel Resonance with internal resistances (ωo only)
2. Self Inductance(L), Mutual Inductance (M), Coefficient of Coupling (k)
3. Natural Current
4. Dot rule
5. Conductively coupled circuits
6. Problems on dot rule directly; Mesh analysis based problems

1. Resonance 

comparison/ Summary:

in detail:

2. L, M, k: (Self Inductance, Mutual Inductances, Coefficient of Coupling):

Self Inductance:

*current in same ckt changes  emf induced, simply,  

i.e. emf self induction ∝ current change

A wire of length l, with N turns has current flowing i through it. 

* Self-induced emf opposes to ckt emf if  i ↑

* Self-induced emf adds to ckt emf if i ↓

e = - L di/dt. ------------(i)

L is the constant of proportionality called Self-inductance.

Faraday's Law:\

e = - N dφ/dt  ------------(ii)

(i)=(ii)

- L di/dt = - N dφ/dt

L =  N dφ/di    ------(iii)

But φ =BA = μH A --->

μH = (μO μr H) A --->

= μO μr NI/l) A --->

L = μO μr N² A/l

Mutual Inductances:

*rate of change of current in one ckt induces emf in another coil; its mutual action; hence the name mutual inductance;]

Flux φ1 produces self-induced voltage e1 in N1 and flux φ12  induces emf e2 in N2

e12= - M21 di1 /dt

e12= - N2 dφ12 /dt       ---- Volts

So 

M21 = N2 dφ12 /di1    ------ (iv)

or

M12 = N1 dφ21 /I1    ------ Henrys

M is called the Mutual Inductance.

Coefficient of Coupling (k):

this means that there is no leakage flux in coil_1; But if flux leakage is there, then a portion k1 of flux φ1  links with turns N2,    

NOTE:

(a) opposing offered in electric circuit---> Resistance

(b) opposing offered in magnetic circuit ---> Reluctance

3. Natural Current:

* Active coil (source v1 connected) = Coil_1

* Passive coil (no source at coil_2) = Coil_2

* Lenz's Law: induced current will appear in such a direction, it opposes the change producing it;

Ex: 

So coil_1 induces emf in coil_2; here two situations on coil_2 side:

• Switch Open---> No current;  So no opposing flux; only induced emf;

• Switch Closed ---> Current flowing in coil_2 is called the "Natural Current"; oppose the coil_1 flux by  coil_2 

The current in the coil_2 follows Right Hand Rule

KVL for loop2: -M di2/dt + L2 di2/dt+ i2 R2 =0

KVL for loop1: - V1- M di1/dt +L1 di1/dt + i1 R1 =0

4. Dot Rule:

* c= coil, d=dot

* dc = dot to coil, the current flows

* similarly cd= coil to dot

Aiding: 

current flow if follows same pattern i.e., dc, dc,... then mutual inductances are said be aiding

or 

current flow if follows same pattern i.e., cd, cd,... then mutual inductances are said be aiding

Opposing: 

current flow if follows different pattern i.e., dc in an inductor and  cd in another,... then mutual inductances are said be opposing

or 

current flow if follows different pattern i.e., cd in an inductor and  dc in another,... then mutual inductances are said be opposing

Example: Series Inductors:

* if the current enters from dot to coil in L1 and from dot to coil in L2, then Mutual inductance (M) is to be used in formula is +ve

* if the current enters from Dot to coil in L1 and from Coil to Dot in L2, then Mutual inductance (M) is to be used in formula is -ve

* Similar analogy can be applied for parallel combination also.

* Inductors can be connected in Series or parallel. Based on these, the following classification is done: 

5. Conductively Coupled Circuits:

From the mesh equations of Magnetically coupled coils, conductively coupled equivalent circuit can be constructed. 

* fig(a) is called magnetically coupled circuit Ex1: Transformer based circuit; Ex2: Inductors between two electrically isolated circuits (but magnetically linked)

*fig(b) is called conductively coupled circuit. Ex: inductors on a single circuit

* for the fig(b) mesh analysis can be applied.

6. Model Problems on conductively coupled circuits:

Example:

Solve the currents I1 and I2.

Solution: 

Voltage source in polar form

12/_60 = 6+10.3923j

Mesh for loop1:

-(6+10.3923j)+5I1 + j2(I1) + j6(I1-I2)- I1(j3)- (I1-I2)(j3)=0

Mesh for loop2:

j6(I2-I1)- j4(I2)+ j3(I1)=0

Solving above equations using Cramer's Rule:

I1= 0.128616+j2.142168 A

I2= 0.192924+j3.214152 A

Quiz Unit-4

1. Formula for Quality factor is ______

2. Fill the below table with appropriate formula:

Parameter	Series Resonance (Series RLC)	Parallel Resonance
		Simple R L C parallel	LC Parallel (Only inductor has internal resistance)	LC Parallel (Both Capacitor and inductor have internal resistances)
Resonant frequency = ωo

Answers:

1. Q= resonant_frequency / Bandwidth =  ωo / (ω2 – ω1)  OR  fo / (f2 – f1)

2. 

Assignment Questions Unit-4

Due date: 11/5/2024

1. A series resonant circuit has R= 100 ohms, L=1mH, C= 10µF. Calculate the bandwidth.

2. Determine the resonant frequency of series resonant circuit.

3. Determine the resonant frequency of parallel resonant circuit.

4. Obtain the equivalent inductance if L1= 3H, L2= 4H, L3=2H, M12= 1H, M23=2H, M13=1H;

5. Determine the currents I1 and I2.

6. Determine the bandwidth of series resonant circuit.

7. Determine the Q-factor of parallel resonant circuit.

8.  Determine the current in the vertical 1mH if frequency of AC source is 1kHz.

Hint:

1mH  --->>> jωL = j*2*π*1000*10-3 = j6.2832Ω

9. Determine the current in the vertical 1mH if frequency of AC source is 2222Hz.

Assignment Key Unit-4

 Q1.

Given Series Resonant, 

R= 100 Ω

L=1mH

C=10µF

Bandwidth = R/L = 100/10^-3 = 100000 rad/sec

Q2.

KVL of a series resonant circuit is:

-Vs + I( R+jωL - j/(ωC))=0

=>

I = Vs/ [ R +j(ωL - 1/(ωC) ] 

In the above equation,resonance occurs if reactance is zero.

i.e., 

ωL - 1/(ωC) = 0  only  if ω=ωo  

ωo L - 1/(ωo C) =0

-->

ωo L = 1/ ωo C

-->

ωo ^2 = 1/(LC)

ωo = 1/ √(LC)

Q3.

Writing current of a parallel resonant circuit is:

=>

I = Vs Y

-->

I= Vs  [ (1/R) +(1/(jωL)) - 1/(j/(ωC)) ] 

In the above equation,resonance occurs if reactance is zero.

i.e., 

- (1/ωL) + ωo C = 0  only  if ω=ωo  

ωo C - 1/(ωo L) =0

-->

ωo C = 1/ ωo L

-->

ωo ^2 = 1/(LC)

ωo = 1/ √(LC)

Q4. 

Given

L1= 3H

L2 = 4H

L3= 2H

M12= 1H

M23= 2H

M13= 1H

Leq= L1 +L2+ L3 - 2M12 + 2M23 -2M13

Q5.

Voltage source in polar form

12/_60 = 6+10.3923j

Mesh for loop1:

-(6+10.3923j)+5I1 + j2(I1) + j6(I1-I2)- I1(j3)- (I1-I2)(j3)=0

Mesh for loop2:

j6(I2-I1)- j4(I2)+ j3(I1)=0

Solving above equations using Cramer's Rule:

I1= 0.128616+j2.142168 A

I2= 0.192924+j3.214152 A

Q6.

At cutoff frequencies,

I=Vs/√2 .

This happens only if imaginary=±real

i.e., 

ωL - 1/(ωC)= ±R     -----(1)

Eq(1) if ωL - 1/(ωC)=R then ω=ω2

Eq(1) if ωL - 1/(ωC)= -R then ω=ω1

ω2 L - 1/(ω2 C)=R 

--->

 ω2 = R±√((RC)^2 + 4L^2 C^2)/ 2LC

Similarly 

ω1 L - 1/(ω1 C)= -R 

--->

 ω1 = -R±√((RC)^2 + 4L^2 C^2)/ 2LC

Bandwidth= ω2-ω1= R/L

Q7.

For a parallel resonant circuit:

Resonant frequency-->

ωo = 1/ √(LC)

Bandwidth--->

BW= 1/(RC)

Quality factor--->

Q=resonant frequency/Bandwidth

i.e., 

Q= ωo /( 1/(RC))   --->

Q= ωo RC

Q8.  Determine the current in the vertical 1mH if frequency of AC source is 1kHz.

Solution:

1mH  --->>> jωL = j*2*π*1000*10-3 = j6.2832Ω

Similarly,

0.4mH --> 2.513jΩ

0.1mH --> 0.62832jΩ

Assume clock-wise currents for both loops;

Mesh for loop1:

-1 + 1000 I1 + 6.283j I1 + (6.283j) (I1- I2) - I2 (0.62832j) - (I1-I2) (2.513j) - I1 (2.513j) =0

-->

I1 (1000 + 7.54j) + I2 (- 4.3983j) =1

Mesh for loop2:

6.2832j (I2-I1)+ 6.283j I2 + 1000 I2 + I1 (2.513j) - I1 (0.6283j) =0

--> 

 I1 (-4.3983j) + I2 (1000+12.566j) = 0

Using Cramer's Rule:

I1 = 0.000999-0.000 007539j A = 0.000999 ∠-0.432 A 

I2 = 0.000 000 08841+ 0.000 004396j A = 0.000004396∠88.84 A

I(vertical1mH) = I1 - I2 = 0.000998∠-0.437 A

Q9. 

1mH  --->>> jωL= j*2*π*f*L = j*2*π*2222*10-3 = j13.96Ω=13.96j Ω

0.1mH ---> 1.396j Ω

0.4mH --> 5.584j Ω

Assume clock-wise currents for both loops;

Mesh for loop1:

-1 + 1000 I1 + 13.96j I1 + (13.96j) (I1- I2) - I2 (1.396j) - (I1-I2) (5.584j) - I1 (5.584j) =0

--->

I1 (1000+16.752j)  + I2 (-9.772j) =1

Mesh for loop2:

13.96j (I2-I1)+ 13.96j I2 + 1000 I2 + I1 (5.584j) - I1 (1.396j) =0

--->

I1 (-9.772j) + I2 (1000+27.92j) = 0

Solving using Cramer's Rule:

I1 = 0.0009996-0.000 0167j A

I2= 0.000 00043599 +0.000 009756j A

Now,

I (vertical1mH) = I1 - I2 = 0.0009995∠-1.516 A

Material Unit-5: Two Port Networks

Topics:
1. Z, Y, ABCD, hybrid parameters
2. Conversion of network parameters
3. Series, Parallel and Cascading of two 2-port networks
4. Image Impedance and Iterative Impedance

General 2-port n/w:

A general two port network comprises of Linear/ bilateral elements and only dependent sources.

It has two ports. Port1 on LHS has inputs V1 and I1. Similarly Port2 on RHS has inputs V2 and I2. Also to remember that I1 is a loop current but not branch current. So I1 enters port1 at 1 and leaves at 1'. Similarly I2 enters at 2 and leaves at 2'. 

 

 

1. Z, Y, ABCD and h-parameters:

2. Conversion of parameters:

Y to Z:

Matrix Z = 1/ Matrix Y

where ∆Y = Y11 Y22 - Y12 Y21

Note: for Z to Y, do same style as above.

Z to ABCD:

ABCD =?

V₁ =A V₂ - B I₂   --(1)

I₁= C V₂ - D I₂  --(2)

Z= known values; So, rewrite Z-parameter equations in the form of ABCD parameter equations.

V₁ =Z₁₁ I₁+ Z₁₂ I₂  --(3)

V₂= Z₂₁ I₁ + Z₂₂ I₂ --(4)

(2) and (4) are similar; but to rewrite (4) in terms of I1; 

I1 = (1/Z₂₁)V₂ - (Z₂₂/Z₂₁) I₂ --(5)

Now(5) = (2)

comparing V2 and I2 coefficients

C=(1/Z₂₁)   and D= (Z₂₂/Z₂₁)

Now substitute (5) in (3) -->

V₁ =Z₁₁ {(1/Z₂₁)V₂ - (Z₂₂/Z₂₁) I₂}+ Z₁₂ I₂  

-->

V₁ =(Z₁₁ /Z₂₁)V₂ - ((Z₁₁ Z₂₂ -Z₂₁ Z₁₂)/ Z₂₁) I₂     where (Z₁₁ Z₂₂ -Z₂₁ Z₁₂)=∆Z

-->

V₁ =(Z₁₁ /Z₂₁)V₂ - (∆Z/ Z₂₁) I₂ --(6)

comparing above equation with (1)

(6) = (1)

-->

A= (Z₁₁ /Z₂₁), B = (∆Z/ Z₂₁)

Z to hybrid:

-use above similar technique to obtain hybrid in terms of Z.

-here Z = known; hybrid= unknown

- equations of  hybrid are (1), (2);

- Z-parameter equations (3), (4);

- (2) = (4); solve this; use this eq(5) to obtain remaining parameters.

Note: Except Z to Y or Y to Z; Remaining all conversions have the 2nd and 4th equation mapped. So easy to solve with internal substitution. 

3. Series, Parallel and Cascading of two 2-port networks:

4. Image and Iterative Impedances:

mage Impedances:

A generator impedance of Zi1 is connected at port1. At port2 , the image impedance is calculated as Zi2. (Or if a generator impedance of Zi2 is connected at port2. At port1 the image impedance is calculated as Zi1)

Zi2= [(Zi1+Za) ∥  Zc]+Zb

Zi2= (Zi1+Za) Zc /((Zi1+Za)+Zc) +Zb

Zi2= {[Zi1 Zc + Za Zc]+ Zi1 Zb + Za Zb +Zc Zb}/(Zi1+Za+Zc)

Similarly Solving for Zi1:

Zi1= [(Zi2+Zb) ∥ Zc]+Za

Zi1= {[Zi2 Zc + Za Zc]+ Zi2 Zb + Za Zb +Zc Zb}/(Zi2+Za+Zc)

Zi1 and Zi2 are called Image impedances.

Note: Zi1=Zi2 iff Za=Zb (i.e., if network is symmetric)

Iterative Impedance:

A generator impedance Zt1 is connected at port1 and Zt2 is impedance observed from port2. Now, this network is connected repeatedly (iterated for multiple times). 

Then the condition for the network to be iterative is Zt1=Zt2. Zt1 and Zt2 are called iterative Impedances. 

Using the below T network, Zt1 is evaluated as:

Zt1=Zt2 as they are iterative impedances

Zt1= [(Zt1+Zb) ∥ Zc]+Za

Zt1= {[Zt1 Zc + Za Zc]+ Zt1 Zb + Za Zb +Zc Zb}/(Zt1 +Za+Zc)

Simplifying , a quadratic equation of Zt1 is obtained.

Quiz Unit-5

1. In the space provided, mention whether the below statement is True/ False.

If two two-port networks (Say X, Y) are connected parallel, then voltages across same end ports of the two networks is same.

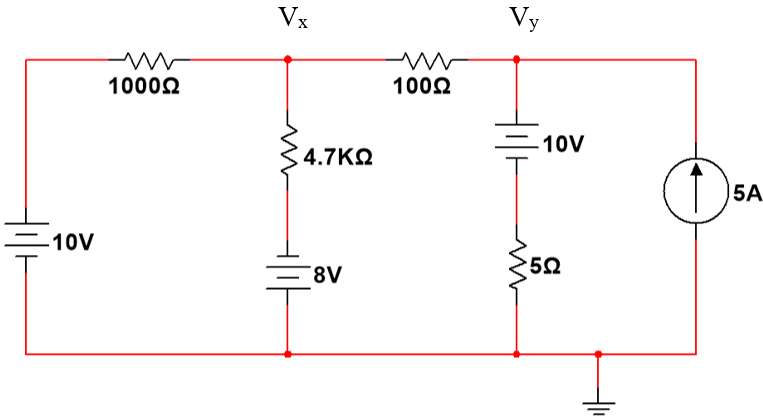
2. In the network given below, with I₂=0. The value of I_b = ______, V₂ = _______

 

Questions 3,4,5,6:

For the given network below, Z₁₁ = ______, Z₂₁ = ______, Z₂₂ = ______, Z₁₂= _____

Questions 7,8,9,10:

 For the network below, the value of Y₁₁ = ____, Y₂₁ = ____, Y₂₂ = ____, Y₁₂= ___

 

11,12,13,14. For the network below, the value of Y₁₁ = ____, Y₂₁ = ____, Y₂₂ = ____, Y₁₂= ___

Answers:

1. True

2. 

 

3, 4, 5, 6.

Z11 = 8+5=13 ohms

Z21= 5 ohms

Z22 =7+5 =12 ohms

Z12 =5 ohms

 

7, 8, 9, 10.

Y11 = 3/2 mhos

Y21 = -1 mhos

Y22 = 4/3  mhos

Y12 = -1 mhos

11, 12, 13, 14:

KCL at V1:

-I1 + V1 (2) + (V1-V2) 1 =0

--> I1 = 3V1 -V2

Y11 = 3℧, Y12= -1℧

similarly

-I2 + V2 (3) + (V2-V1)1 =0

-->

Y21 = -1℧, Y22= 4℧

Assignment Questions Unit-5

Due date: 27/4/2023

1. Determine the Z-parameters of the network

2. Determine the Z-parameters of the network

3. Two networks shown in below figure are connected in series. Determine the Z-parameters.

4. Convert Z-parameters to Y-parameters.

5. Convert h-parameters to ABCD-parameters.

6.  Determine h-parameters for below two-port network.

7. Determine Z-parameters for the below network. R1= 6Ω , R2= 9Ω, R3 =8Ω ,R4=12Ω.

8. If two two-port-networks x and y are connected in parallel, determine the overall admittance parameters of the network.

9. Determine the Y-parameters of the below network.

R1= 150Ω , R2= 470Ω, R3 =47Ω

Assignment Key Unit-5

Q1. 

Applying Mesh analysis for loop1:

V1 = I1 (Z1+Z3)+ I2 (Z3)

Applying Mesh analysis for loop2:

V2 = I1 (Z3) + I2 (Z3+Z2)

Comparing above equations ith Z-parameter equations:

Z11 = Z1 + Z3

Z12 = Z3

Z21 = Z3

Z22 = Z3+Z2

Q2. 

in the middle loop, assume I3 (clock-wise) current

Mesh for loop1:

-V1 + Z1 (I1 - I3)=0 ---(1)

Mesh for last loop:

-V2 + Z3 (I2+I3)= 0  ---(2)

Mesh for middle loop:

Z1(I3-I1) + Z2 I3 + Z3 (I3+I2) =0

-->

I3 (Z1+Z2+Z3) = I1 Z1 - I2 Z3

-->

I3 = I1 [ Z1/(Z1+Z2+Z3)] - I2 [Z3/(Z1+Z2+Z3)]    ---(3)

Substitute (3) in (1)

and

Substitute (3) in (2)

Now compare  the V1 and V2 obtained above with that of z-parameter equations to obtain Z-parameters.

Z11 =

Z12=

Z21=

Z22=

Q3.

Network(a)

Z-parameters:

Z11a= 12 ohms

Z12a= 8 ohms

Z21a= 8 ohmms

Z22a= 12 ohms

Network(b)

Z-parameters:

Z11b= 24 ohms

Z12b= 16 ohms

Z21b= 16 ohmms

Z22b= 24 ohms

For series connection of networks (a), (b):

Z11= Z11a+Z11b = 1121+24= 36 ohms

Z12 =Z12a+Z12b= 8+16= 24 ohms

Z21= Z21a+Z21b = 8+16= 24 ohms

Z22= Z22a+Z22b = 12+24= 36 ohms

Q4.

Convert Z to Y parameters (means Z are known values, Y are unknown) 

Always operate on known equations:

Z-parameter equations:

V1= Z11 I1 + Z12 I2      --(1)

V2= Z21 I1 + Z22 I2      ---(2)

Y-parameter equations are:

I1 = Y11  V1 + Y12 V2   ---(x)

I2 = Y21 V1 + Y22 V2  ---(y)

from (2) 

I2 = (1/Z22) V2 -(Z21/Z22) I1 ---(3)

substitute (3) in (1)

V1 = Z11 I1 + Z12 [(1/Z22) V2 -(Z21/Z22) I1]

rearranging 

V1 = [(Z11 Z22 - Z12 Z21)/Z22] I1 + (Z12/Z22) V2

-->

V1 = (∆Z/Z22) I1 + (Z12/Z22) V2

-->

I1 = (Z22/∆Z) V1 - (Z12/∆Z) V2  ---(4)

(4)=(x)

---> 

Y11 = Z22/∆Z,  Y12 = -Z12/∆Z

Substitute (4) in (1)

I2= 

Y21 = , Y22 = 

Express Z in terms of Y (Y are known parameters, Z are unknown parameters)

Always operate on known equations:

Z-parameter equations:

V1= Z11 I1 + Z12 I2      --(x)

V2= Z21 I1 + Z22 I2      ---(y)

Y-parameter equations are:

I1 = Y11  V1 + Y12 V2   ---(1)

I2 = Y21 V1 + Y22 V2  ---(2)

from(2) write V2

i.e.,

Y22 V2 = I2 - Y21 V1

-->

V2 = (1/Y22) I2- (Y21/Y22) V1 ----(3)

substitute (3) in (1)

I1 =Y11 V1 + Y12 [(1/Y22) I2- (Y21/Y22) V1]

I1 = Y11 V1 + (Y12/Y22) I2 - (Y21 Y12/Y22)V1

-->

I1 = (Y11 Y22/ Y22)V1 +(Y12/Y22) I2 - (Y21 Y12/Y22)V1

--> 

I1 = V1 [Y11 Y22- Y12 Y21]/Y22  + (Y12/Y22) I2

-->

I1 = V1 (∆Y/Y22) + (Y12/Y22) I2

-->

 V1 = (Y22/∆Y) I1 - (Y12/∆Y) I2   ---(4)

(4)=(X)

So, Z11 = Y22/∆Y 

Z12 = Y12/∆Y

Substitute (4) in (1)

then rearrange to obtain V2.

Now write:

Z21 = 

Z22 =

Q5. 

known parameters are hybrid

unknown are ABCD

Always operate on known parameters.

h-parameter equations:

V1 = h11 I1 + h12 V2   ----(1)

I2 = h21 I1 + h22 V2   ---(2)

ABCD parameter equations:

V1 = A V2 - B I2   ---(3)

I1 = C V2 - D I2   ---(4)

(2) and (4) are similar

express (2) in the form of (4)

I1 = (1/h21) I2 - (h22/h21) V2

i.e.,

I1 = (-h22/h21) V2 + (1/h21) I2   ---(5)

Now

(5)=(4)

i.e.,

C= -h22/h21 , D= -1/h21

Substitute (5) in (1)

and simplify to obtain in the below form:

V1 =   (   ) V2   +   (  ) I2

-->

A =

B= 

Q6. 

hybrid parameter equations are:

V1 = h11 I1 + h12 V2   ----(1)

I2 = h21 I1 + h22 V2   ---(2)

Writing Z-parameter equations for the given network:

V1 = 58 I1 + 50 I2    ---(3)

V2 = 50 I1 + 70 I2   ---(4)

to obtain h-parameters from z-parameters:

(4) and (2) are similar

-->

from(4) write I2

I2 = (1/70)V2 - (50/70) I1

i.e.,

I2 = (-50/70) I1 + (1/70) V2 ---(5)

(5)=(2)

i.e., h21 = -50/70

and

h22 = 1/70 mhos

Substitute (5) in (3)  and write V1 equation from it

V1= 58 I1 + 50 [ (-50/70) I1 + (1/70) V2]

-->

V1= (1560/70) I1 + (50/70) I2 ---(6)

(6)=(1)

-->

h11 = 1560/70 ohms

h12 = 50/70

Q7.

Mesh for loop1:

-V1 + R1 (I1- I3) + R3 (I1+I2) =0   ---(1)

Mesh for loop2:

-V2 + R2 (I2+I3) + R3 (I2 +I3) =0   ---(2)

Mesh for loop3:

R1(I3-I1) + R4 (I3) + R2 (I3+I2) =0

--->

I3 (R1+R2+R4) = I1 R1 - I2 R2

-->

I3 = [R1/(R1+R2+R4)] I1 - [R2/(R1+R2+R4)] I2 =0 ----(3)

substitute (3) in (1) to obtain Z11, Z12

substitute (3) in (2) to obtain Z21, Z22

Z11 =

Z12 =

Z21 =

Z22 = 

Q8.

In parallel networks, Voltages are same but current will split.

Voltage:

Port1 for both networks has voltage V1 i.e., V1a  = V1b =V1

and Port2 for both networks has voltage V2 i.e., V2a =V2b = V2

Current:

Main current I1 will split as currents  I1a and I1b i.e., I1 = I1a + I1b

similarly current I2 will split as currents  I2a and I2b i.e., I2 = I2a + I2b

Network -(a)  Y-parameters are:

I1a = Y11a V1 + Y12a V2     ---(1)

I2a = Y21a V1 + Y22a V2     ---(2)

Network -(b)  Y-parameters are:

I1b = Y11b V1 + Y12b V2     ---(3)

I2b = Y21b V1 + Y22b V2     ---(4)

So adding (1) and (3)

I1a + I1b = I1 = V1 (Y11a + Y11b) + V2 (Y12a + Y12b)     ---(5)

Similarly adding (2) and (4)

I2a + I2b = I2 = V1 (Y21a + Y21b) + V2 (Y22a + Y22b)     ---(6)

from(5) and (6)

Y11 = Y11a + Y11b

Y12= Y12a + Y12b

Y21 = Y21a + Y21b

Y22 = Y22a + Y22b

Q9. 

Y-parameter equations are:

I1 = Y11  V1 + Y12 V2   ---(x)

I2 = Y21 V1 + Y22 V2  ---(y)

Nodal at V1:

-I1 + V1/ R1 + (V1-V2)/R2 =0

rearranging 

I1 = V1 [1/R1 + 1/R2] - V2[1/R2]        ---(1)

Nodal at V2:

-I2 + V2/R3 + (V2-V1)/R2 = 0

rearranging

I2 = V1 [-1/R2] + V2 [1/R2  + 1/R3]       ---(2)

comparing (1) and (2) with Y-parameter equations (x),(y)

Y11 =

Y12=

Y21 =

Y22= 

Important points that repeat in every unit

---Steady State (units- 1,2,4,5)-----

Ohms Law= Voltage at resistor= V= IR
Voltage at inductor = V= I (jωL)
Voltage at capacitor = V = I [-j/(ωC)]

-----------------------

---Transients (unit-3)-----

Ohms Law= Voltage at resistor= V= i(t) R
Voltage at inductor = V= L di(t)/dt
Voltage at capacitor = V = (1/C) ∫ i(t) dt

-----------------------

k=kilo = 10³

M=Mega= 10⁶

G=Giga= 10⁹

T =Tera= 10¹²

m= milli= 10^-3

μ = micro= 10^-6

n= nano= 10^-9

p= pico= 10^-12

-------------------------

Vab = Va - Vb

GATE/ NET Exam info

GATE2020 to GATE2021: Circuit analysis: Node and mesh analysis, superposition, Thevenin's theorem, Norton’s theorem, reciprocity. Sinusoidal steady state analysis: phasors, complex power, maximum power transfer. Time and frequency domain analysis of linear circuits: RL, RC and RLC circuits, solution of network equations using Laplace transform. Linear 2-port network parameters, wye-delta transformation.

GATE 2022:Circuit analysis: Node and mesh analysis, superposition, Thevenin's theorem, Norton’s theorem, reciprocity. Sinusoidal steady state analysis: phasors, complex power, maximum power transfer. Time and frequency domain analysis of linear circuits: RL, RC and RLC circuits, solution of network equations using Laplace transform. Linear 2-port network parameters, wye-delta transformation.

GATE 2023:
Circuit Analysis: 

(i) Node and mesh analysis, 

(ii) superposition, Thevenin's theorem, Norton’s theorem, reciprocity. 

(iii) Sinusoidal steady state analysis: phasors, complex power, maximum power transfer. 

(iv)Time and frequency domain analysis of linear circuits: RL, RC and RLC circuits, solution of network equations using Laplace transform. 

(v) Linear 2-port network parameters, 

(vi) wye-delta transformation. 

ACE coaching- Link 

PreviousPapers and Key 

PDF materials - Link 

GATE Standard books -Link

GATE Pattern for ECE:
Marks (Questions)= 100M (65Q) = 15M (10Q on GA) + 85M (55Q on EC)
NOTE: 15M for GA + (12 to 15M for Engg Maths) +( 73 to 70M for EC)
Questions pattern= MCQ, MSQ, NA
Negative marking = Mark/3; Example: if its 2M question, then negative marking is 2/3.
NOTE: Negative marking for MCQ only.